小Y是一个充满智慧的女孩子，但是她只会使用串并联的方法计算两个节点之间的电阻。

现在小Y有一个电阻网络，问有多少点对 $(u,v)(u\ne v)$ 之间的电阻可以用串并联的方法计算出来。

我们来形式化地定义一下点对 $(u,v)(u\ne v)$ 之间的电阻能否用串并联的方法计算出来。首先我们把电阻网络看成一个 $n$ 个点 $m$ 条边的图（每个电阻对应一条边）。令 $S$ 表示从 $u$ 到 $v$ 的所有简单路径(不经过重复的点的路径)上点的并集，也就是对于一个点 $x$ ，如果存在一条从 $u$ 到 $v$ 的简单路径经过这个点，那么它就在集合 $S$ 中。如果 $S$ 非空且 $S$ 的导出子图是 $u,v$ 为端点的二端串并联图，那么 $u,v$ 之间的电阻就能用串并联方法计算。

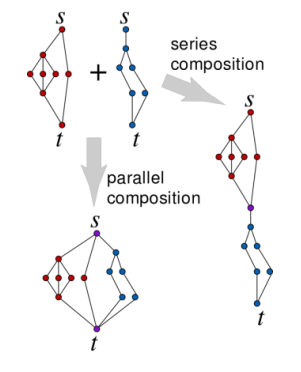
一个有两个不同端点 $s,t$ 的图被称为二端图，其中一个称为源点，另一个称为汇点。两个二端图 $X,Y$ 并联(parallel composition)是指建一个新图，把 $X$ 和 $Y$ 的源点和汇点分别合并起来。两个二端图 $X,Y$ 串联(series composition)是指建一个新图，把 $X$ 的汇点和 $Y$ 的源点合并起来。由若干个两个点一条边的二端图经过一系列串并联变化之后形成的图称为二端串并联图。

集合 $S$ 的导出子图点集为 $S$ ，边集由原图中两个端点都在 $S$ 中的边构成。

输入格式

第一行包含 $2$ 个正整数 $n,m$ ，表示电阻网络中的节点数和电阻数。

接下来 $m$ 行，每行包含 $2$ 个正整数 $u,v(1\le u,v\le n,u\ne v)$ ，表示有一个电阻在节点 $u$ 和 $v$ 之间。

输出格式

输出共 $1$ 行，表示答案，即有多少点对之间的电阻可以使用串并联的方法计算出来。

样例一

input

6 6
1 2
1 3
1 4
2 3
2 4
5 6

output

6

explanation

可行的点对有 $(1,2),(1,3),(1,4),(2,3),(2,4),(5,6)$。

样例二

input

13 18 
1 2 
2 3 
2 4 
3 4 
3 5 
4 5 
5 6 
5 7 
5 8 
6 8 
7 8 
8 9 
10 11 
10 12 
10 13 
11 12 
11 13 
12 13

output

25

样例三

见样例数据下载。

样例四

见样例数据下载。

限制与约定

时间限制：$1\mathtt{\text{s}}$

空间限制：$256\mathtt{\text{MB}}$

下载

样例数据下载