南极的冰山下冰冻着许多奥秘。为了一探究竟，跳蚤国王选定了一大片富含远古微生物的冰山样本，准备将其切割成小片以供研究。

冰山样本是一片面积巨大的矩形冰片。放置在地上时，可视为占据了平面直角坐标系的整个第一象限 $[0, +\infty) \times [0, +\infty)$。

为了切割冰片，跳蚤国王放置了 $n+m$ 个激光发射器：

• 其中有 $m$ 个竖直向上的激光发射器，第 $i$ 个竖直向上的激光发射器位于 $(i,0)$，所发出的激光的强度为 $10^{100}$；
• 其中有 $n$ 个水平向右的激光发射器，第 $i$ 个水平向右的激光发射器位于 $(0,i)$，所发出的激光的强度为 $l_i$。

这里的激光发射器都是为切割冰片而量身定制的。所发射的激光在空气中几乎无法传播，但在冰中可以正常穿行，并会产生极高的温度。

最开始，所有光束发射器都是关闭的。在一次操作中，操作员需要按照某种顺序将它们依次激活。当一个发射器被激活时，它会瞬间向它所对应的方向发出一束激光。该激光会不断沿该射线方向延伸，直到触碰到另一束激光已经融化过的点（即接触到空气），或延伸距离到达了这个激光发射器所发出的的激光的强度。然后在很短的时间内，该激光所经过的路径上的冰会同时融化，从而达到切割的效果。

例如，$m=n=3,\ l_1=1,\ l_2=4,\ l_3=2$ 时，如果依次激活位于 $(3,0),(0,2),(2,0),(0,3),(0,1),(1,0)$ 的光束发射器，那么最后冰片被激光切割后的效果如下图：

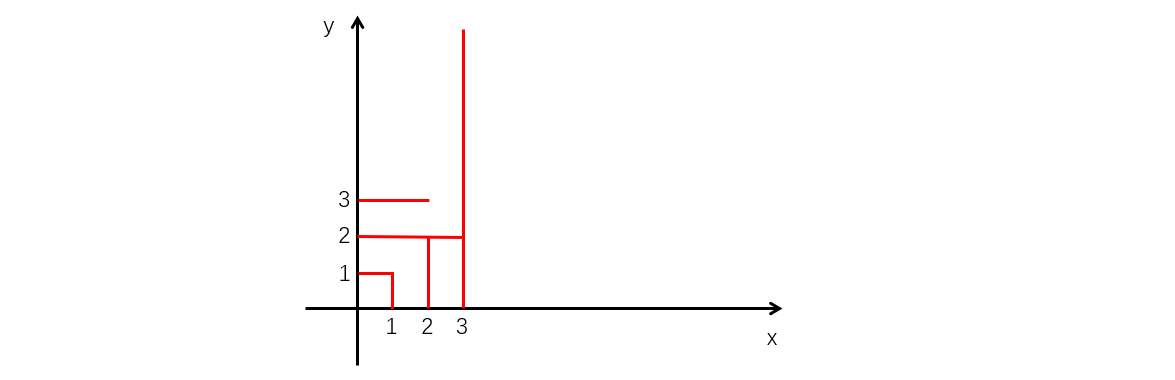
物理学家伏特把玩起了这些发射器。伏特发现，开关发射器的顺序不同，切割的结果也不相同。伏特想要知道，若可以以任意顺序依次激活所有光束发射器，总共可以得到多少种不同的切割结果？两种切割结果是不同的，当且仅当冰片上被融化的点所组成的集合不相同。

由于伏特还在忙着把玩这些发射器，因此你需要帮助伏特计算出本质不同的方案数。由于方案数可能很多，因此你只需要告诉他答案对 $998244353$ 取模后的结果。

输入格式

输入的第一行包含两个整数 $m,n$。

接下来一行，包含 $n$ 个整数 $l_1,\ldots,l_n$。

输出格式

输出一行一个整数，表示答案。

样例一

input

3 3
1 4 2

output

11

样例二

input

10 10
7 8 5 8 3 2 3 4 4 6

output

2021

样例三

见附件下载。该样例满足子任务 3 的限制。

样例四

见附件下载。该样例满足子任务 4 的限制。

样例五

见附件下载。该样例满足子任务 5 的限制。

数据范围

对于 $100\%$ 的数据：$1\leq m\leq 10^9,\ 1\leq n\leq 500,\ 1\leq l_i\leq 10^9$。

时间限制：$1\texttt{s}$

空间限制：$512\texttt{MB}$