关羽喜欢下象棋!
不过这次,他下腻了传统象棋,并叫来了你做他的对手。你们将在一张
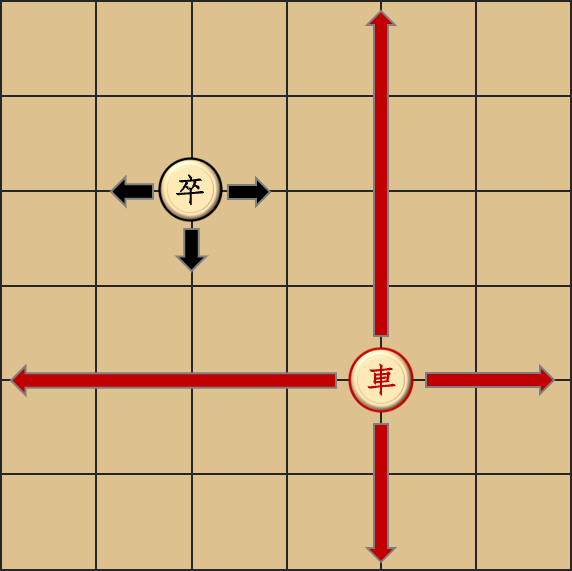
- 卒初始在第
- 卒每次可以在左、右、下三种移动方向中选择一种,然后移动一格(但是不能往上)。即,若记第
- 车可以向左向右移动多格,也可以向上向下移动多格,也可以不动。即,车可以从
- 卒和车均不可以走到棋盘外。
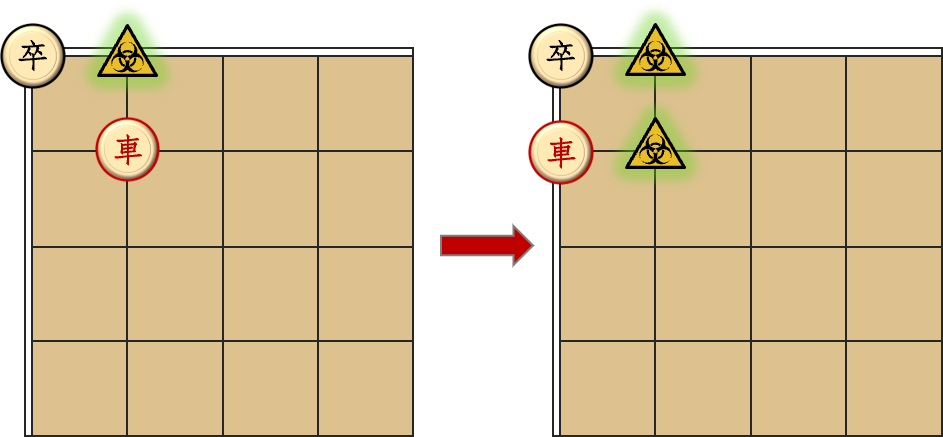
- 这辆车经过现代科技改造,会沿路散发毒气,车经过的格点都会被毒雾覆盖,卒不能停留。例如,如果车从
- 这辆车不可被摧毁,即卒不能吃车,也不能移动到车占据的位置。
聪明的你发现你可以因此吊打武神关羽!于是你非常好奇,你最快几步可以击败关羽。这个特殊的象棋分为若干回合,每回合是这样进行的:
- 你操控车移动一次,也可以选择不动。
- 如果车吃掉了卒(即车占据了卒所在位置),游戏结束。
- 卒移动一步。当且仅当卒没有可移动方向时,卒才可以选择不动(即左、右、下三个方向均为车、毒气、棋盘边界中的一种)。例如,如果进行到某一轮前,
游戏总回合数定义为车决策的次数。
当然武神也很聪明,他希望游戏回合数尽可能多,而你希望游戏回合数尽可能少,并且你们都足够聪明。你想提前知道,游戏将会进行几回合?
输入格式
第一行一个整数
接下来
输出格式
样例一
input
4 1 1 2 2 1 2 2 4 100 50 3 3 50 2 49 4
output
2 3 2 3
explanation
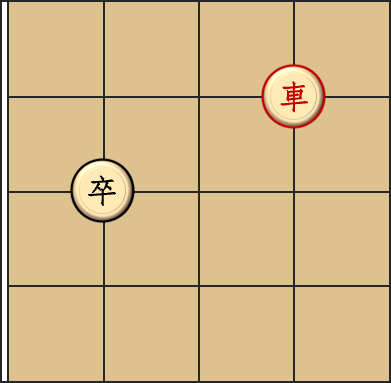
对于第一组数据,车可以选择停在原地,而轮到卒的时候卒必须移动。无论向下还是向右,都会立马被车吃掉。
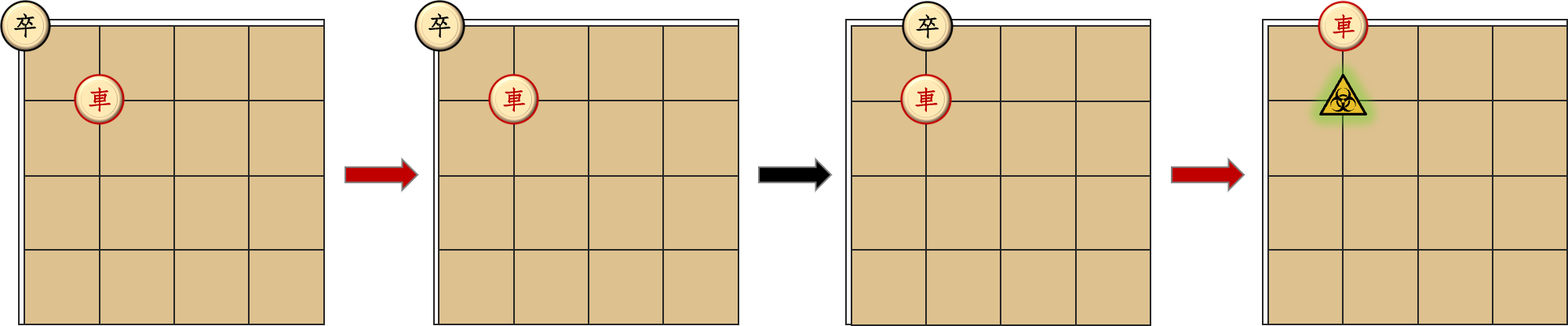
注意这里只画了棋盘左上角。
对于第二组数据,车可以先在卒下方洒出一行毒雾,然后再走到卒所在的第一行,即可必杀。
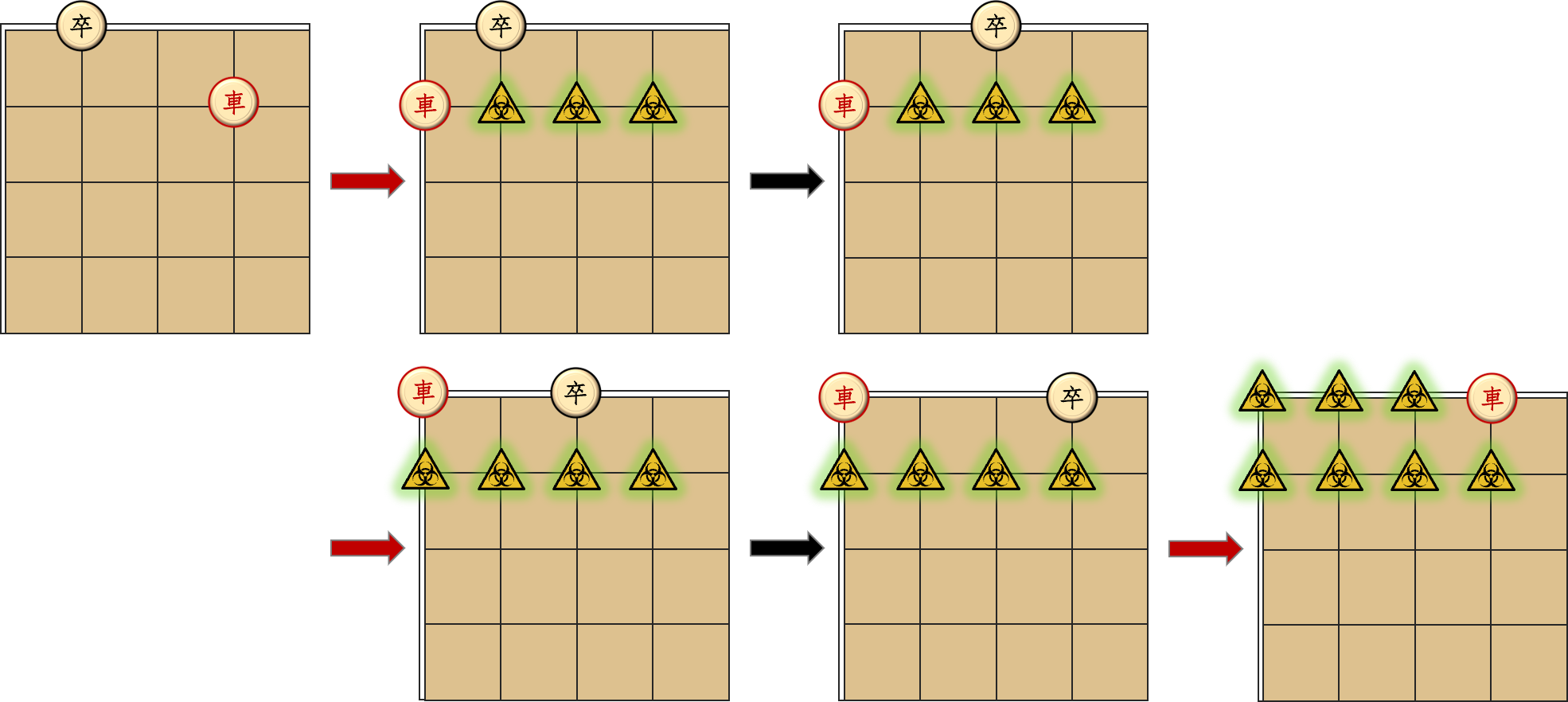
对于第三组数据,车移动到
对于第四组数据,答案是
样例二
input
13 72 75 73 56 59 55 60 56 59 70 59 65 82 66 82 62 97 2 98 6 97 2 98 15 63 79 64 82 57 71 58 75 96 64 97 66 96 73 97 76 96 99 95 97 96 99 88 98 98 100 100 99
output
3 3 1 1 3 3 3 3 3 3 3 3 2
数据范围与提示
| 子任务编号 | 特殊性质 | 分值 |
|---|---|---|
| 无 |
对于所有数据,
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号