小 z 给小 m 出了一道毒瘤题。
小 m 并不会做，于是小 m 开始写暴搜。虽然小 z 曾经说过：理论复杂度和运行效率没有直接关系，但是小 m 还是想知道，暴搜的理论复杂度。她发现，她的搜索次数是在一棵树上填数的方案数。
这棵树有 $10^{10^{10}}$ 个节点，从 $1$ 开始编号。设 $r \ge 1$ 为一个参数。对于编号为 $i$ 的节点，如果 $2\leq i\leq r + 1$，那么它的父亲是编号为 $i-1$ 的节点；如果 $r + 2\leq i$，它的父亲是编号为 $i-2$ 的节点。
下图是一棵 $r=4$ 的树，只画出了顶上的一小部分。每个圆圈为一个节点，圆圈旁边标的数为这节点的编号。
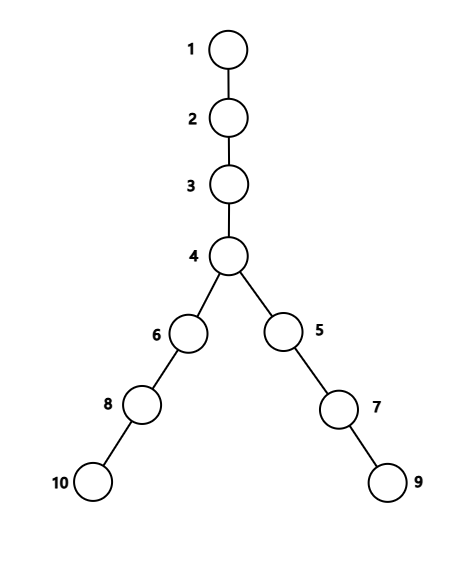
现在小 m 想给每个节点都填进一个数。填数需要满足三个条件：
- 填的数都是非负整数。
- 对于第 $i(2\leq i)$ 个节点，它父亲填的数必须不小于它。
- 所填数之和恰好为 $n$。
小 m 想知道，对于 $n\in [1,N]$，有多少种方法填数。然而她也意识到了方案数非常大，因此你只需要输出答案对 $998244353$ 取模后的结果。
输入格式
一行两个整数 $N,r$ 分别表示数之和的最大值和树的形态。
输出格式
一行 $N$ 个整数，第 $i$ 个整数表示 $n=i$ 时的方案数对 $998244353$ 取模后的结果。
样例一
input
9 4
output
1 2 3 5 8 14 22 36 56
explanation
对于 $n=5$，方案如下：
- $[5]$
- $[4,1]$
- $[3,2]$
- $[3,1,1]$
- $[2,2,1]$
- $[2,1,1,1]$
- $[1,1,1,1,1]$
- $[1,1,1,1,0,1]$
其中第 $i$ 个数表示第 $i$ 个节点填的数，未标出部分均填 $0$。
样例二
见附件下载。
数据范围与提示
| 子任务编号 | $N\leq$ | $r\leq$ | 分值 |
|---|---|---|---|
| $1$ | $100$ | $20$ | $10$ |
| $2$ | $1000$ | $100$ | $20$ |
| $3$ | $500000$ | $1$ | $10$ |
| $4$ | $2$ | $30$ | |
| $5$ | $500$ | $30$ |
对于所有数据，$1\leq N\leq 500000,1\leq r\leq 500$。
时间限制：$\texttt{3s}$
空间限制：$\texttt{512MB}$
鄂公网安备 42010202000505 号