小 Q 是一名设计师，她精心设计了一个公园。经过两年的努力，这个公园终于修建完毕。她十分开心，邀请了她的朋友小 P 一起来游览这个公园。她们兴致勃勃地制定了很多游览计划。但是，她们发现这些计划太过宏大，她们有可能没有精力去完成这些计划。她们想通过一个程序来评估一下这些计划需要花费的精力，然而她们的编程能力有限，所以她们想让你帮忙解决这个问题。

公园有 $n$ 个景点，$m$ 条连接两个景点的无向道路。第 $i$ 条道路连接第 $x_i$ 和第 $y_i$ 个景点，其长度为 $l_i$。公园的线路是小 Q 精心设计的，小 Q 保证她设计的公园中从任意一个景点出发，能够到达所有的景点；保证每条道路连接的是两个不同的景点；保证没有两条不同的道路连接同一对景点；并且对于任意四个不同的景点 $A,B,C,D$，都不能找到六条路径，使得其中任意两条路径除公共端点外没有公共点，且这六条路径分别连接四个景点中的每一对景点—— $AB,AC,AD,BC,BD,CD$。

以下给出一些一定不是小 Q 设计的公园线路图的例子：

（ $1$ 号景点不能到达 $3$ 号景点）

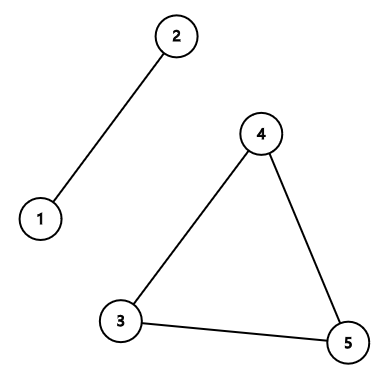
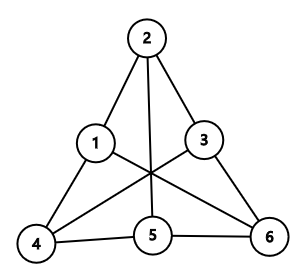
（对于第 $1,4,5,6$ 号景点，存在六条除端点外两两没有公共点的路径 $1\rightarrow4,4\rightarrow5,5\rightarrow6,6\rightarrow1,4\rightarrow3\rightarrow6,1\rightarrow2\rightarrow5$ 连接这四个景点的每一对景点）

小 P 她们制定出了 $q$ 个不同的计划，对于第 $i$ 个计划，她们选择了 $k_i$ 个不同的景点 $a_{i,1},a_{i,2},\cdots,a_{i,k_i}$ 准备游览。

设 $dis(x,y)$ 为景点 $x$ 和景点 $y$ 之间的最短路径长度，对于第 $i$ 个计划，你需要回答：

对于每一组不同的 $(i_1,i_2) \ (i_1 \leq i_2)$ ，景点 $a_{i,i_1}$ 和 $a_{i,i_2}$ 之间最短路长度之和 $\bmod 2013265921$ ，即求 $$\sum_{i_1=1}^{k_i-1} \sum_{i_2=i_1+1}^{k_i} dis\left(a_{i,i_1},a_{i,i_2}\right)\bmod 2013265921$$

输入格式

第一行两个正整数 $n,m$。

接下来 $m$ 行，每行三个正整数，其中第 $i$ 行表示 $x_i,y_i,l_i$，即第 $i$ 条道路的连接的两个景点和其长度。

第 $m+2$ 行一个非负整数 $q$。

接下来 $q$ 组询问，每组形如以下两种之一：

为上述第一种询问，第一行一个正整数 $k_i$，表示选择的景点个数。接下来一行 $k_i$ 个整数 $a_{i,1},a_{i,2},\cdots,a_{i,k_i}$，表示选择的景点。

输出格式

对于每一个询问输出一行一个非负整数表示该询问的答案。

样例一

input

2 1
1 2 5
1
2
1 2

output

5

限制与约定

保证 $2\le n \le 10^5$, $1 \le q \le 10^5$, $\sum k_i \le 10^5$。

保证 $x_i,y_i,a_{i,j} \le n$, $l_i \le 10^9$。

按照常理，公园是有出入口的。但是在本题中，你可以认为公园的出入口也是景点。

定义环路为起点和终点相同，并且中间（即除起点终点外）不经过重复景点的路径上道路的集合。

子任务 1（5 分）：$n \le 1000$, $\sum k_i \le 3000$；

子任务 2（5 分）：$q=1$，$m=n-1$；

子任务 3（20 分）：$m=n-1$；

子任务 4（10 分）：$k_i=2$，保证每条道路最多属于一个环路；

子任务 5（10 分）：保证每条道路最多属于一个环路；

子任务 6（10 分）：保证删去第 $m$ 条道路后每条道路最多属于一个环路；

子任务 7（25 分）：$k_i = 2$；

子任务 8（15 分）：无特殊限制。

时间限制：$8\texttt{s}$

空间限制：$1024\texttt{MB}$

本题时间限制较大，测试点个数较多，建议自行特判无法通过的测试点，求不虐萌萌哒评测机！

下载

样例数据下载