火车司机出秦川,跳蚤国王下江南。每天,勤劳的火车司机们都会开着自己心爱的火车去传播福音。
和跳蚤国类似,火车国也有 个城市编号为 到 ,城市之间有一些铁路相连。这些铁路构成了一个仙人掌。如果一个无向连通图的任意一条边最多属于一个简单环,我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。
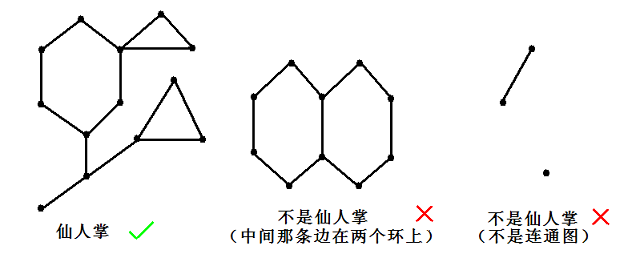
第 天会有 名火车司机出秦川,第 名司机会从城市 到 。有一些司机是老司机,他们会沿着选择经过城市最多的路径走,显示自己高超的驾驶技术。而另一些是新司机,他们会走经过城市最少的路径。但不管是新司机还是老司机,都不会走过同一个城市两次(也就是选择的路径都是简单路径)。
每一条铁路周围都有一些人居住,如果第 天这条铁路被火车司机经过,这些人会收到福音。我们想知道每天有多少人收到福音。
当然人口是会变化的,第 天结束以后第 铁路的人口会改变为 。
输入格式
第一行三个整数 和 ,表示有 个城市,有 条铁路以及有 天。
接下来 行每行三个整数 ,表示一条连接 和 的铁路,铁路周围有 个人。保证是仙人掌,没有自环,每个环的长度都是奇数。铁路编号从 开始。
接下来 行,每两行表示一天。
第一行一个整数 表示有 名司机( 可能为 ,这时候请忽略这个询问并输出 ),然后是 个整数 ,分别表示每个司机的起点和终点和类型,如果 是 表示是新司机,为 是老司机。每个司机的起点和终点均不同。
第二行两个整数 和 ,表示第 条铁路的人口会改变为 ,如果 为 则表示没有修改。
输出格式
行,每行一个整数表示这一天收到福音的人数。
样例一
input
11 13 3
1 2 1
2 3 2
1 3 4
2 8 8
2 9 16
9 10 32
10 11 64
11 9 128
3 4 256
3 5 512
4 7 1024
7 6 2048
5 6 4096
1 10 7 1
3 8192
3 8 1 1 2 7 1 10 4 0
7 16384
3 8 1 0 2 7 0 10 4 1
0 16384
output
6869
15163
32667
样例二
见样例数据下载。
样例三
见样例数据下载。
限制与约定
保证任意时刻边长和都属于int范围内。边长均为正整数。
, ,令 , 。
具体数据范围见下表:
| 数据编号 |
的规模 |
的规模 |
的规模 |
其他 |
|---|
| 1 | | | | 无 |
| 2 | | | |
| 3 | | | | ,没有修改 |
| 4 | |
| 5 | | | | ,没有修改 |
| 6 | |
| 7 | | | | 没有修改 |
| 8 | 无 |
| 9 | | | | 没有修改 |
| 10 | 无 |
时间限制:
空间限制:
下载
样例数据下载
IOI赛制
本题在考试时排行榜上显示的成绩即为最终评测结果。


 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号