由于电信技术的发展，信息的交换变得十分方便。

现在有 $n$ 个人，依次编号为 $1, \dots, n$。初始时第 $i$ 个人手机里存储着编号为 $i$ 的气泡熊表情。由于对自己的表情并不十分满意，他们计划进行一次大交换。

这 $n$ 个人中有一些朋友关系，可以抽象为一个简单无向图 $G$。简单无向图即无重边无自环的无向图。

每个人有三种状态：不满，激动，满意。初始时均为不满。

有一个神秘人，操纵他们按如下方式行动：

function dfs(v):
    v 变为激动状态
    for u = 1, ..., n:
        if v 和 u 是朋友 and u 处于不满状态:
            交换 v 和 u 的手机中的气泡熊表情
            dfs(u)
    v 变为满意状态

for v = 1, ..., n:
    if v 处于不满状态:
        dfs(v)

一万万年后，一位考古学家调查了最终每个手机中存储的气泡熊表情的编号，想要复原出朋友关系图 $G$。然而这几乎是不可能的，所以他想知道有多少种可能的 $G$。

输入格式

第一行一个正整数 $n$。

第二行包含 $n$ 个整数 $a_1, \dots, a_n$，表示最终第 $i$ 个人的手机上存储的气泡熊表情编号。保证 $a_1, \dots, a_n$ 是一个 $1$ 到 $n$ 的排列。

输出格式

一行，一个整数表示 $G$ 的数量，你只用输出答案对 $998244353$（$7 \times 17 \times 2^{23} + 1$，一个质数）取模后的结果。

样例一

input

3
2 3 1

output

2

explanation

共以下两种：

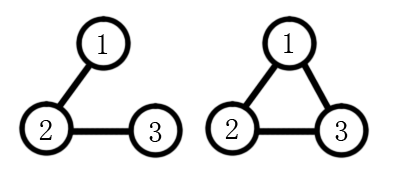
样例二

input

9
7 2 9 1 3 8 6 5 4

output

3528

样例三

见样例数据下载。

限制与约定

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

下载

样例数据下载