wangyisong1996 有一棵小树苗，可惜由于土地沙漠化小树苗枯死了。正当 wangyisong1996 悲痛欲绝的时候，从沙子中长出了一棵仙人掌。

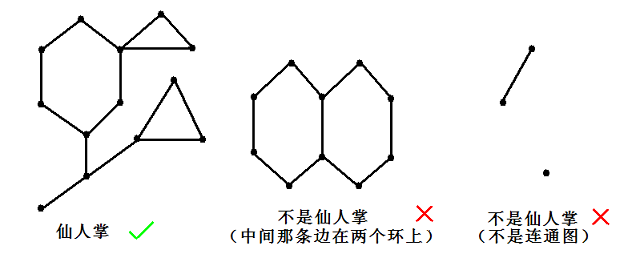
如果一个无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。

有一棵 $n$ 个结点的仙人掌，每条边有一个长度 $l$。（不同的边的长度不一定相同）

有 $q$ 个点集，每个点集可以用两个整数 $u, d$ 来描述（$1 \leq u \leq n$），一个结点 $v$ 在这个点集中当且仅当结点 $v$ 与结点 $u$ 的距离不超过 $d$。两个结点之间的距离为它们之间的最短路径的长度。

现在要求构造一个有向无环图（DAG），满足：

1. 这个 DAG 至少有 $n+q$ 个结点，至多有 $1200000$ 个结点和 $2400000$ 条边。
2. 对于每一条边，如果是从 $u$ 连向 $v$ 的，那么 $u > n$ 且 $u \neq v$。
3. 对于结点编号在第 $i$ 个点集（$1 \leq i \leq q$）的每一个结点 $x$，第 $n+i$ 个结点到第 $x$ 个结点有且仅有一条路径。
4. 对于结点编号在 $\{ 1, 2, \dots, n\}$ 中但不在第 $i$ 个点集（$1 \leq i \leq q$）的每一个结点 $x$，不存在第 $n+i$ 个结点到第 $x$ 个结点的路径。

输入格式

第一行三个正整数 $n, m, q$，其中 $n, m$ 表示这棵仙人掌一共有 $n$ 个结点 $m$ 条边。

接下来 $m$ 行，每行三个整数 $u,v,l$，表示 $u$ 和 $v$ 之间有一条长度为 $l$ 的无向边。保证 $1 \leq u, v \leq n$。

接下来 $q$ 行，第 $i$ 行表示第 $i$ 个点集，用两个整数 $u, d$ 来描述，保证 $1 \leq u \leq n$。

输出格式

第一行两个非负整数 $V,E$，表示你构造的 DAG 的点数和边数。

接下来 $E$ 行，每行两个整数 $u,v$，表示 $u$ 到 $v$ 有一条有向边。你需要保证 $1 \leq u, v \leq V$。

样例一

input

10 9 5
2 1 9553
3 2 8499
4 3 5171
5 1 7123
6 3 1904
7 5 5526
8 7 5853
9 6 6635
10 8 7858
6 4981
7 14400
3 21290
4 9451
10 16609

output

15 19
11 6
11 3
12 7
12 5
12 1
12 8
12 10
13 3
13 6
13 9
13 4
13 2
13 1
14 4
14 3
14 6
15 10
15 8
15 7

限制与约定

对于每一条边，$1 \leq l \leq 10000$。对于每个点集，$0 \leq d \leq 10^9$。

第 2 个测试点的生成方式：

for i in range(2, 10001):
    addedge(i, i / 2)

第 3 个测试点的生成方式：

for i in range(2, 5000):
    addedge(i, i - 1)
for i in range(5000, 10001):
    addedge(i, randint(1, i - 1))

其中 range(l,r) 表示区间 $[l,r)$ 中的所有数，randint(l,r) 返回一个在 $[l,r]$ 内的随机整数。

addedge(u, v) 表示在 $u$ 和 $v$ 间连一条边。（边的长度的生成方式，你以为我会告诉你吗？）

时间限制：$1\texttt{s}$

空间限制：$256\texttt{MB}$

来源

中国国家集训队互测2015 - By 王逸松

下载

样例数据下载