在日本，城市是用一个高速公路网络连接起来的。这个网络包含 $ N $ 个城市和 $ M $ 条高速公路。每条高速公路都连接着两个不同的城市。不会有两条高速公路连接相同的两个城市。城市的编号是从 $ 0 $ 到 $ N - 1 $，高速公路的编号则是从 $ 0 $ 到 $ M - 1 $。每条高速公路都可以双向行驶。你可以从任何一个城市出发，通过这些高速公路到达其他任何一个城市。

使用每条高速公路都要收费。每条高速公路的收费都会取决于它的交通状况。交通状况或者为顺畅， 或者为繁忙。当一条高速公路的交通状况为顺畅时，费用为 $ A $ 日元（日本货币），而当交通状况为繁忙时，费用为 $ B $ 日元。这里必有 $ A < B $。注意，$ A $ 和 $ B $ 的值对你是已知的。

你有一部机器，当给定所有高速公路的交通状况后，它就能计算出在给定的交通状况下，在两个城市 $ S $ 和 $ T $（ $ S \ne T $ ）之间旅行所需要的最小的高速总费用。

然而，这台机器只是一个原型。所以 $ S $ 和 $ T $ 的值是固定的（即它已经被硬编码到机器中），但是你并不知道它们的值是什么。你的任务就是去找出 $ S $ 和 $ T $ 的值。为了找出答案，你打算先给机器设定几种交通状况，然后利用它输出的高速费用来推断出 $ S $ 和 $ T $。由于设定高速公路交通状况的代价很大，所以你并不想使用这台机器很多次。

实现细节

你需要实现下面的过程：

find_pair(int N, int[] U, int[] V, int A, int B)

• N: 城市的数量。
• U及V: 长度为 $ M $ 的数组，其中 $ M $ 为连接城市的高速公路的数量。对于每个 $ i $ ( $ 0 \le i \le M - 1 $)，高速公路 $ i $ 连接城市 U[i] 和 V[i]。
• A: 交通状况顺畅时高速公路的收费。
• B: 交通状况繁忙时高速公路的收费。
• 对于每个测试样例，该过程会被调用恰好一次。
• 注意，$ M $ 为数组的长度，可以按照注意事项的相关内容来取得。

过程 find_pair 可以调用以下函数:

int64 ask(int[] w)

• w 的长度必须为 $ M $。 数组w描述高速公路的交通状况。
• 对于每个 $ i $（ $ 0 \le i \le M - 1 $ ），w[i] 表示高速公路 $ i $ 的交通状况。 w[i] 的值必须为 $0$ 或 $1$。
  • w[i] = 0 表示高速公路 $ i $ 的交通状况为顺畅。
  • w[i] = 1 表示高速公路 $ i $ 的交通状况为繁忙。
• 该函数返回的是，在w所描述的交通状况下，在城市 $ S $ 和 $ T $ 之间旅行所需的最少总费用。
• 该函数最多只能被调用 $ 100 $ 次 （对于每个测试样例）

find_pair 应调用以下过程来报告答案：

answer(int s, int t)

• s 和 t 的值必须为城市 $ S $ 和 $ T $（两者的先后次序并不重要）。
• 该过程必须被调用恰好一次。

如果不满足上面的条件，你的程序将被判为 $\texttt{Wrong Answer}$。否则，你的程序将被判为 $\texttt{Accepted}$， 而你的得分将根据 ask 的调用次数来计算（参见子任务）。

例子

设 $ N = 4 $, $ M = 4 $, $ U = [0, 0, 0, 1] $, $ V = [1, 2, 3, 2] $, $ A = 1 $, $ B = 3 $, $ S = 1 $ 和 $ T = 3 $。

评测程序调用 find_pair(4, [0, 0, 0, 1], [1, 2, 3, 2], 1, 3)。

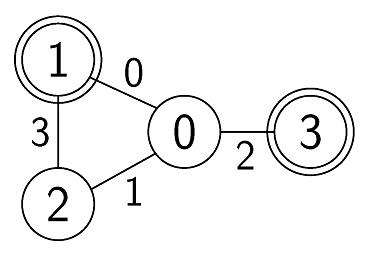
上图中，编号为 $ i $ 的边对应高速公路 $ i $。其中一些对ask的可能调用和对应的返回值如下表所示:

对于函数调用 $ \texttt{ask([0, 0, 0, 0])} $，所有高速公路的交通状况均为顺畅，因此每条高速公路的费用都是 $ 1 $。从城市 $ S $ 到城市 $ T $ 的费用最低的路径就是 $ 1 \rightarrow 0 \rightarrow 3 $。这条路径的总费用等于 $ 2 $。因此，这个函数的返回值就是 $ 2 $。

对于一个正确的解答来说，过程find_pair应调用answer(1, 3)或answer(3, 1)。

在样例数据下载中的文件ex_highway1.in对应于本例。其他的输入样例在样例包中还可找到。注意：样例包中的输出没有任何意义。

限制条件

• $ 2 \le N \le 90\ 000 $
• $ 1 \le M \le 130\ 000 $
• $ 1 \le A < B \le 1\ 000\ 000\ 000 $
• 对于每个 $ 0 \le i \le M - 1 $
  • $ 0 \le U[i] \le N - 1 $
  • $ 0 \le V[i] \le N - 1 $
  • $ U[i] \ne V[i] $
• $ (U[i], V[i]) \ne (U[j], V[j]) $ 且 $ (U[i], V[i]) \ne (V[j], U[j]) $ ($ 0 \le i < j \le M - 1 $)
• 你可以从任何一个城市出发，通过高速公路到达其他任何一个城市。
• $ 0 \le S \le N - 1 $
• $ 0 \le T \le N - 1 $
• $ S \ne T $

在本题中，评测程序不是适应性的。意思是说，在评测程序开始运行的时候 $ S $ 和 $ T $ 就固定下来，而且不依赖于你的程序所做的询问。

子任务

1. (5 分) $ S $ 或 $ T $ 有一个是 $ 0 $, $ N \le 100 $, $ M = N - 1 $
2. (7 分) $ S $ 或 $ T $ 有一个是 $ 0 $, $ M = N - 1 $
3. (6 分) $ M = N - 1 $, $ U[i] = i $, $ V[i] = i + 1 $( $ 0 \le i \le M - 1 $ )
4. (33 分) $ M = N - 1 $
5. (18 分) $ A = 1 $, $ B = 2 $
6. (31 分) 没有附加限制。

假设你的程序被判为 $\texttt{Accepted}$，而且函数ask调用了 $ X $ 次。你在该测试样例上的得分 $ P $，取决于对应子任务的编号，其计算如下：

• 子任务 1： $ P = 5 $.
• 子任务 2： 如果 $ X \le 60 $，$ P = 7 $。否则 $ P = 0 $。
• 子任务 3： 如果 $ X \le 60 $，$ P = 6 $。否则 $ P = 0 $。
• 子任务 4： 如果 $ X \le 60 $，$ P = 33 $ 。否则 $ P = 0 $。
• 子任务 5： 如果 $ X \le 52 $，$ P = 18 $ 。否则 $ P = 0 $。
• 子任务 6：
  • 如果 $ X \le 50 $，$ P = 31 $ 。
  • 如果 $ 51 \le X \le 52 $，$ P = 21 $。
  • 如果 $ 53 \le X $，$ P = 0 $。

注意，你在每个子任务上的得分，等于你在该子任务中所有测试样例上的最低得分。

请注意：在测试中，如果你的程序在一个子任务中某个点未获得满分，则可能会得到 $ 0 $ 分。在 hack 中，程序会优先将你给出的输入匹配为编号最小的子任务。。

评测程序示例

评测程序示例将读取如下格式的输入：

• 第 $ 1 $ 行：$ N \ M \ A \ B \ S \ T $
• 第 $ 2 + i $ 行 ( $ 0 \le i \le M - 1 $ )：$ U[i] \ V[i] $

如果你的程序被判为$\texttt{Accepted}$，评测程序示例将打印出$\texttt{Accepted: q}$，这里的$q$为函数ask被调用的次数。

如果你的程序被判为$\texttt{Wrong Answer}$，它打印出$\texttt{Wrong Answer: MSG}$。各类$\texttt{MSG}$的含义如下：

• answered not exactly once：过程answer没有被调用恰好一次。
• w is invalid：传给函数ask的w的长度不是 $ M $，或者某个 $ i $（ $ 0 \le i \le M - 1 $ ）上的w[i]既不是 $ 0 $ 也不是 $ 1 $。
• more than 100 calls to ask：函数 ask 的调用次数超过 100 次。
• {s, t} is wrong：调用answer时的s和t是错的。

约定及限制

对于所支持的各种编程语言，下面列出了对应的数据类型。对于数据类型的细节等，参见实现示例。

时间限制：$2\texttt{s}$

空间限制：$268\texttt{MB}$

下载

样例数据下载