在咕了无数锅和 ddl 之后,S***pe 终于如愿以偿,变成了一只翱翔在天空中的白鸽。S***pe 很久以前听说过,白鸽的使命,就是以不同的方向飞过天空,带给地上的人们无尽的灵感。可是刚刚被变成白鸽的 S***pe 心理并不平衡,他远远地看见了地面上那个甩锅给他的人 w*x,他决定不给 w*x 提供应该提供的灵感,而且 S***pe相信不给灵感的方法就是绕着 w*x 顺时针转圈,这样的话对于 w*x 来说白鸽就只有往右侧飞行,而不能看到白鸽以不同的方向飞过天空了。
S***pe 觉得自己的行程必须经过若干个关键点,他请你帮他规划路线。
简而言之,现在在二维平面上,有一个给定一张
在这张图上的每个节点都在二维平面上有自己的坐标,而一条边对应了连接这两个点的线段,S***pe 的目标是从
顺时针旋转的次数:假设 w*x 在 S***pe 飞行的过程中始终保持正面朝向 S***pe,那么在 S***pe 结束飞行之后 w*x 原地右转的圈数就是顺时针旋转的次数(可以为负)。
如果无解输出
输入格式
第一行两个正整数
接下来
接下来
输出格式
一行一个整数,如果是
样例一
input
5 10 1 9 6 -8 9 7 -5 -10 10 -6 1 3 3 4 2 3 1 4 5 2 4 5 1 3 3 1 4 1 3 1
output
2
explanation
样例中的图如下图所示,注意图中的重边未被标识。
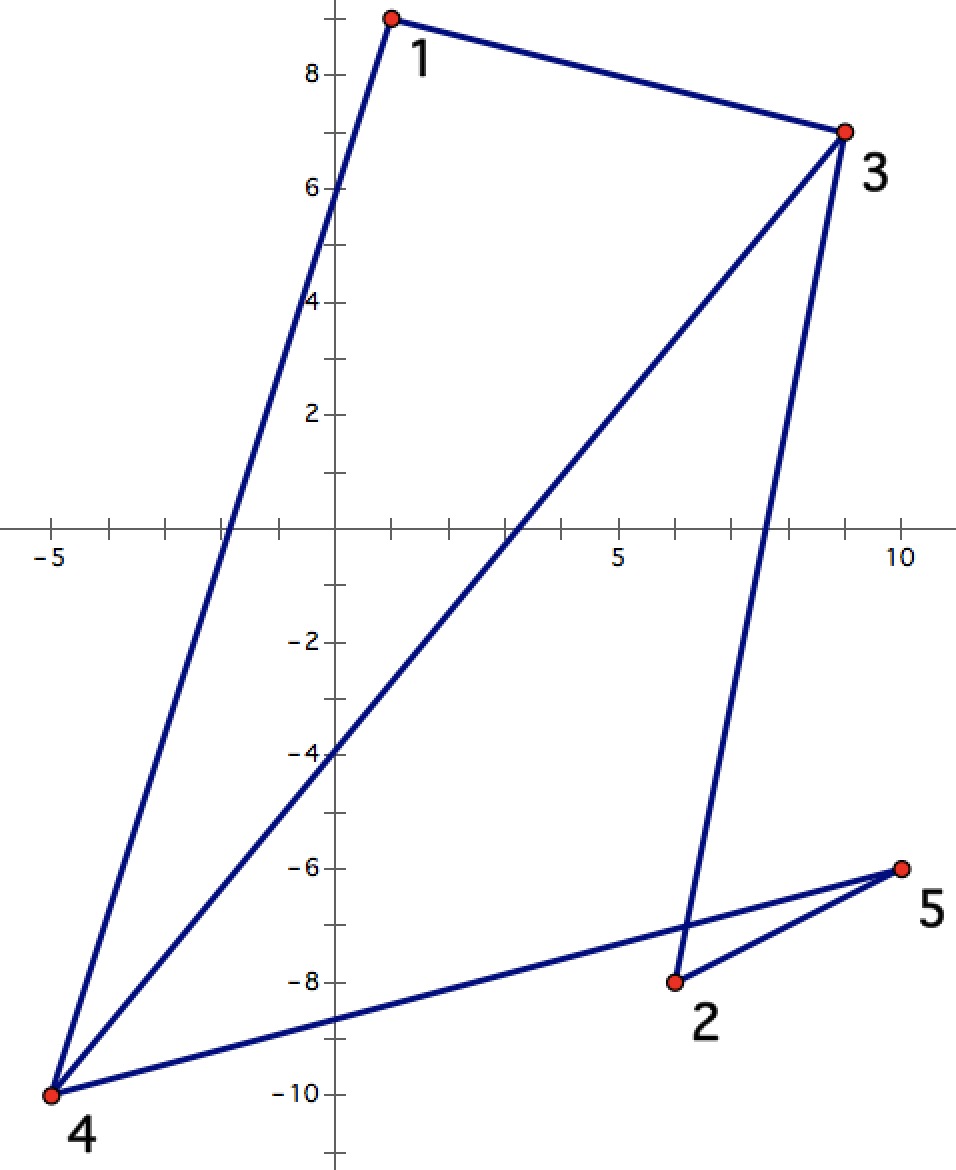
一种最优的遍历顺序是:
再次提醒:注意重边。
样例二
input
3 5 -764351767 899476675 103147230 -443149366 432530806 578822602 2 3 2 3 1 3 3 1 2 3
output
-1
explanation
不存在满足条件的路径。
样例三
见样例数据下载。
样例四
见样例数据下载。
限制与约定
对于所有数据,
| 子任务 | 分值 | 限制 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号