哈萨克斯坦有 $N$ 座小城镇,编号从 $0$ 到 $N - 1$,另有不知道具体数量的若干大城市。哈萨克斯坦的这些小城镇和大城市统称为定居点。
哈萨克斯坦的所有定居点通过一个双向公路网络连接在一起。每条公路连接 $2$ 个不同的定居点。每对定居点之间最多有一条直接相连的公路。对于任意一对定居点 $a$ 和 $b$,只要经过的公路最多只能使用一次,则有一条唯一的路径从 $a$ 走到 $b$。
每个小城镇只能与另外一个定居点直接相连,而大城市与 $3$ 个或者更多的定居点直接相连。
下图给出了一个由 $11$ 个小城镇和 $7$ 个大城市组成的网络。小城镇用圆圈表示并用整数编号,大城市用方形表示并用字母标识。
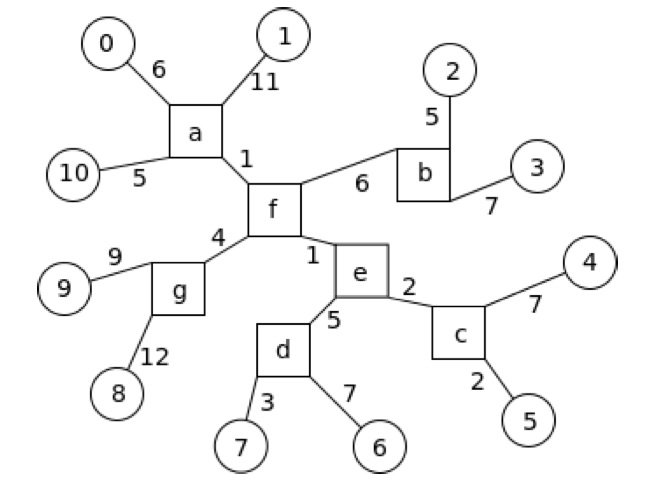
每条公路的长度都是一个正整数。两个定居点之间距离是从一个定居点走到另一个定居点所经过的所有公路长度之和的最小值。
对于大城市 $C$,$r(C)$ 表示离 $C$ 最远的小城镇到 $C$ 的距离。在所有的大城市中 $r(C)$ 值最小的大城市称为中心城市(hub)。离中心城市最远的小城镇到中心城市的距离是 $R$,即 $R$ 是所有 $r(C)$ 的最小值。
在上例中,离大城市 $a$ 最远的小城镇是城镇 $8$,大城市 $a$ 和小城镇 $8$ 之间的距离 $r(a) = 1 + 4 + 12 = 17$。对于大城市 $g$ 来说,$r(g) = 17$(距离大城市 $g$ 最远的小城镇之一是城 $6$)。上图中唯一的中心城市是城市 $f$,其 $r(f)=16$,因此上例中 $R$ 是 $16$。
删除某个中心城市后,整个网络会分成几个连通子图,如果每个子图中至多包含 $\lfloor N / 2 \rfloor$ 个小城镇,那么这个删除的中心城市就是平衡的(balanced)。注意:计数中不含大城市,$\lfloor x \rfloor$ 表示不大于 $x$ 的最大整数。
在上例中,大城市 $f$ 是一个中心城市,如果删除 $f$,整个网络分成 $4$ 个连通子图,这 $4$ 个子图分别包含下列小城镇 ${0, 1, 10}, {2, 3}, {4, 5, 6, 7}$ 和 ${8, 9}$,没有任何一个子图包含超过 $\lfloor 11 / 2 \rfloor = 5$ 个小城镇,所以大城市 $f$ 是一个平衡的中心城市。
任务
最初,整个网络的唯一信息只有小城镇的数目 $N$。你不知道大城市的数目,也不清楚公路的网络连接情况。你获取信息的唯一方法是查询两个小镇之间的距离。
你的任务是确定:
- 在所有的子任务中:距离 $R$。
- 子任务 $3$ 到 $6$:网络中是否存在平衡的中心城市。
你需要实现函数 hubDistance。Grader 将会在一次运行中评测多个测试点。每次运行时最多有 $40$ 个测试点。对每个测试点,grader 会调用你的函数 hubDistance 恰好一次。请确保你的函数在每次被调用时都初始化所有需要的变量。
hubDistance(N, sub)- N: 小城镇的数目。
- sub: 子任务编号(详见子任务描述部分)。
- sub是 $1$ 或者 $2$ 时,该函数返回 $R$ 或 $-R$ 均可。
- sub大于 $2$ 时,如果存在平衡的中心城市,该函数返回 $R$,否则返回 $-R$。
你的 hubDistance 函数可以通过调用 grader 函数 getDistance(i, j) 而获得关于公路网络的信息。函数 getDistance(i, j) 返回小城镇 $i$ 与小城镇 $j$ 之间的距离。注意:如果 $i$ 和 $j$ 相同的话,函数的返回值将是 $0$,而且当参数不合法时,返回值也是 $0$。
子任务
对每个测试点而言: $N$ 的范围是 $[6, 110]$。 两个小镇之间距离的范围是$[1, 1000000]$。
你调用 getDistance(i, j) 函数查询的次数是有一定限制的。该限制与子任务有关,详见下表。如果你的程序调用的次数超过限制,你的程序将会被终止,且视为答案错误。
| 子任务 | 分数 | 查询次数限制 | 是否查找平衡中心城市 | 限制 |
|---|---|---|---|---|
| 1 | 13 | $\frac{n(n - 1)}{2}$ | 否 | 无 |
| 2 | 12 | $\lceil \frac{7n}{2}\rceil$ | 否 | 无 |
| 3 | 13 | $\frac{n(n - 1)}{2}$ | 是 | 无 |
| 4 | 10 | $\lceil \frac{7n}{2}\rceil$ | 是 | 每个大城市都刚好与 $3$ 个定居点连接 |
| 5 | 13 | $5n$ | 是 | 无 |
| 6 | 39 | $\lceil \frac{7n}{2}\rceil$ | 是 | 无 |
注意:$\lceil x \rceil$ 表示大于或等于 $x$ 的最小整数。
实现细节
你只能提交一个源文件实现如上所述的 hubDistance 函数,并且遵循下面的命名和接口。你需要包含头文件 towns.h。
int hubDistance(int N, int sub);评测方式
请注意子任务的编号也是输入的一部分。grader 根据子任务的编号而改变它评分的方法。
- 第 $1$ 行:子任务编号和测试点的数目。
- 第 $2$ 行:$N_1$,第一个测试点中小城镇的数目。
- 接下来的 $N_1$ 行:第 $i$ 行($1 \le i \le N_1$)第 $j$ 个($1 \le j \le N_1$)数字是小城镇 $i - 1$ 到小城镇 $j - 1$ 的距离。
- 随后是下一个测试点的数据,格式与第 $1$ 个测试点的数据相同。
对于每个测试点,grader 会在不同行上输出函数 hubDistance 的返回值及调用函数的次数。
本题样例的输入格式如下:
1 1 11 0 17 18 20 17 12 20 16 23 20 11 17 0 23 25 22 17 25 21 28 25 16 18 23 0 12 21 16 24 20 27 24 17 20 25 12 0 23 18 26 22 29 26 19 17 22 21 23 0 9 21 17 26 23 16 12 17 16 18 9 0 16 12 21 18 11 20 25 24 26 21 16 0 10 29 26 19 16 21 20 22 17 12 10 0 25 22 15 23 28 27 29 26 21 29 25 0 21 22 20 25 24 26 23 18 26 22 21 0 19 11 16 17 19 16 11 19 15 22 19 0
时间限制:$1\texttt{s}$
空间限制:$1500\texttt{MB}$

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号