【清华集训2015】遥远的星系 - 题目

小 m 的星系中有 $n$ 颗有人居住的星球。起初这些星球之间的距离过于遥远，一个人无法在有生之年到达另一个星球，移民往往是几代人接力完成，旅游、看望族裔更是无从谈起。

后来，五维生物为人们建立了空间翘曲轨道。穿越轨道的人会感觉自己瞬间便到达了目的地，但对于外界来说，时间已经发生了巨大的变化，可能过去了几千年，也可能倒退几千年。

形式化地讲，可以用3个数描述一条轨道： $u, v, w$ ，表示这条轨道连接了星球 $u$ 和星球 $v$ ，若从 $u$ 穿过轨道到达 $v$ ，时间会改变 $w$ ；若从 $v$ 穿过轨道到达 $u$ ，时间会改变 $- w$ 。注意到 $w$ 可正可负，当时间改变为正时，表示会经过这么长时间；为负值时，表示会倒流这么长时间；为零则表示时间不会变化。

有了轨道以后，人们便可以实现到其他星球的短期旅行，但同时也催生了新的需求：希望在特定时间到达某个星球，以看到特定的人或看到特定的历史事件。为了达到这一需求，人们可以经过任意多条轨道，在穿越多个星球以后到达目的地。

形式化地讲，可以用3个数描述一条需求： $u, v, w$ ，表示希望从星球 $u$ 出发，到达星球 $v$ ，与出发时间相比，中途的时间改变为 $w$ （注意这里的 $w$ 也可正可负）。

现在的问题是，给出轨道的建立过程和过程中所有的需求，问每条需求是否能得到满足。

具体地，你将依次得到 $m$ 条操作，每条操作为建立一条轨道或一条需求。若为一条需求，你需要回答只使用需求之前的所有轨道，“能”还是“不能”完成这个需求。

输入输出格式

你可以不用理会后面提到的输入输出文件的真实格式，仅用这里提到的方法进行输入输出。

首先将 maze_io.cpp 中的代码粘贴到你的代码的最开头。

你的程序首先需要调用 maze_io::get_args(&n, &m, &k, &t); 获取4个参数。其中 $n$ 和 $m$ 如前文所述， $k$ 和 $t$ 为跟数据格式相关的参数。注意四个变量必须都定义为 int 类型。

接下来需要调用 $m$ 次 maze_io::get_line(&p, &u, &v, &w); 获取4个参数。其中 $p$ 表示操作的类型， $0$ 表示新建轨道， $1$ 表示一条需求，剩余3个变量意义如前文所述。注意 $p, u, v$ 必须定义为 int 类型， $w$ 必须定义为 long long 类型。

对于每条需求，你需要调用一次 maze_io::put_ans(ans); 来输出一次答案。其中 $a n s$ 是 int 类型，值为 $0$ （表示不能完成需求）或 $1$ （表示能完成需求）。

若 $k = 3$ ，表示你必须输出答案以后才能获取下一个操作，否则没有这个限制；若 $k = 0$ ，表示所有的需求操作一定排在所有新建轨道操作之后。

将所有轨道视为无向边。若 $t = 0$ ，表示最终所有的轨道构成森林；若 $t = 1$ ，表示最终轨道构成的任何一个连通块中，至多只有一个环；若 $t = 2$ ，表示最终所有轨道构成一片仙人掌林，即每条边至多属于一个简单环；若 $t = 3$ ，则没有特殊约束。

由于输出为传入的参数 $a n s$ 本身，因此我们可以用 maze_sample.cpp 输出样例实际的操作（会从 maze.in 和 maze.ans 读入，输出到 maze.h.in），输出格式为：第一行包含四个整数 $n, m, k, t$ ，接下来 $m$ 行，每行包含4个整数 $p, u, v, w$ 。

如果你希望自己构造测试的输入数据，那么格式为：第一行包含四个整数 $n, m, k, t$ ，接下来 $m$ 行，每行包含6个整数 $p, u, v, w, x, y$ ，令 $x = y = 0$ 即可。

样例一

input

5 20 3 3
0 5 2 8 737023109 467551616
0 1 3 -11 610666965 103793774
1 5 2 10 801050508 81540882
0 4 4 -9 432795277 577469097
0 4 1 17 167617173 189172213
0 1 4 -20 1005183139 269123299
1 4 3 -3 305267432 348822094
1 3 5 17 957086530 565704649
0 5 5 -13 580644467 252604773
0 3 5 9 262777226 184032246
1 2 1 14 438439996 597179973
0 1 4 7 489012768 974964269
1 5 1 2 660680201 894637208
1 2 2 2 682205686 450663892
1 3 5 8 181963596 230165952
0 5 2 16 673556059 931780532
0 5 4 -3 507063636 1066313785
1 5 2 -10 493798980 249901807
1 3 3 8 248671409 626524461
1 3 2 -8 159081180 345560641

output

explanation

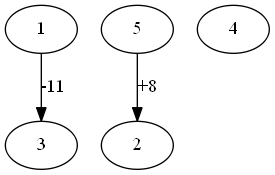
graph1

对于第 $1$ 个需求， $5$ 到 $2$ 只有一条轨道，时间会 $+ 8$ ，无法满足 $+ 10$ 的需求。

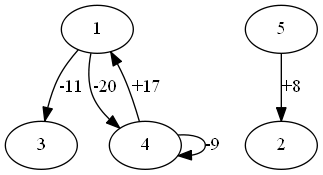
graph2

对于第 $2$ 个需求，路线从 $4$ 开始， $- 9$ 到达 $4$ ， $+ 17$ 到达 $1$ ， $- 11$ 到达 $3$ ，总计为 $- 3$ 。

对于第 $3$ 个需求，路线从 $3$ 开始， $+ 11$ 到达 $1$ ， $+ 20$ 到达 $4$ ， $- 17$ 到达 $1$ ， $+ 20$ 到达 $4$ ， $- 17$ 到达 $1$ ，总计为 $+ 17$ 。

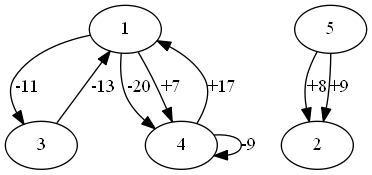
graph3

对于第 $5$ 个需求，虽然 $1$ 附近的区域轨道很多，但是无论如何都无法做到回到 $1$ 时时间 $+ 2$ 。

限制与约定

对于所有的数据，最终获取到的所有数都是整数，且满足 $1 \leq u, v \leq n$ ， $p \in {0, 1}$ 。

各测试点满足下列限制：

测试点	$n =$	$m =$	$k =$	$t =$	$\| w \| \leq$
1	$5$	$20$	$3$	$3$	$20$
2	$50$	$200$	$3$	$3$	$20$
3	$10^{5}$	$10^{6}$	$2$	$0$	$10^{12}$
4	$10^{5}$	$10^{6}$	$3$	$0$	$10^{12}$
5	$10^{5}$	$10^{6}$	$0$	$1$	$10^{12}$
6	$10^{5}$	$10^{6}$	$2$	$1$	$10^{12}$
7	$10^{5}$	$10^{6}$	$3$	$1$	$10^{12}$
8	$10^{5}$	$10^{6}$	$3$	$1$	$10^{12}$
9	$10^{5}$	$10^{6}$	$0$	$2$	$10^{12}$
10	$10^{5}$	$10^{6}$	$2$	$2$	$10^{12}$
11	$10^{5}$	$10^{6}$	$2$	$2$	$10^{12}$
12	$10^{5}$	$10^{6}$	$3$	$2$	$10^{12}$
13	$10^{5}$	$10^{6}$	$0$	$3$	$10^{12}$
14	$10^{5}$	$10^{6}$	$0$	$3$	$10^{12}$
15	$10^{5}$	$10^{6}$	$2$	$3$	$10^{12}$
16	$10^{5}$	$10^{6}$	$2$	$3$	$10^{12}$
17	$10^{5}$	$10^{6}$	$2$	$3$	$10^{12}$
18	$10^{5}$	$10^{6}$	$3$	$3$	$10^{12}$
19	$10^{5}$	$10^{6}$	$3$	$3$	$10^{12}$
20	$10^{5}$	$10^{6}$	$3$	$3$	$10^{12}$

时间限制： $2 s$

空间限制： $1 GB$

输入输出文件的补充说明

不用理解这段话也可以完成这道题目。

实际的输入输出文件是对输入添加了简单的防离线处理得到的，你可以通过阅读 maze_io.cpp 中的代码得到这个处理方法。你完全可以不使用这段代码进行输入输出，而使用自己的方法（例如你想要使用更快速的输入输出方法或你希望利用防离线处理的漏洞）。我们保证最终数据的格式和样例的格式是相同的，不会有反“反防离线”的处理。

具体地，各参数（指代码中 scanf 读入的各数）的数据规模为： $1 \leq u, v \leq n$ ；当 $k = 3$ 时， $0 \leq x, y < 2^{30}$ ；否则 $x = y = 0$ 。这些数均为整数。其他参数约束同“数据规模及约定”。

Universal Online Judge

UOJ

#155. 【清华集训2015】遥远的星系