小 E 同学非常喜欢书法，他听说 NOI2013 已经开始了，想题一幅 “NOI” 的字送给大家。

小 E 有一张非常神奇的纸，纸可以用一个 $n$ 行 $m$ 列的二维方格矩阵来表示，为了描述方便，我们定义矩阵左下角方格坐标为 $(1,1)$，右上角方格坐标为 $(m, n)$。

矩阵的每个方格有一个整数的幸运值。在格子上面写字可以增加大家的幸运度，幸运度的大小恰好是所有被笔写到的方格的幸运值之和。现在你要在上面写上 “N”, “O”, “I” 三个字母。

下面给出 $3$ 个书法字的定义:

1. “N” 由若干 （$\geq 3$） 个边平行于坐标轴的矩形组成，设由 $K$ 个矩形组成（标号 $1 \sim K$），第 $i$ 个矩形的左下角方格坐标设为 $(L_i, B_i)$，右上角坐标设为 $(R_i, T_i)$，要求满足：
   • $L_i \leq R_i, B_i \leq T_i$
   • 对任意 $1 < i \leq K$，有 $L_i = R_{i−1} + 1$
   • 对任意 $3 \leq i < K$，有 $B_{i−1} − 1 \leq T_i \leq T_{i−1}$，$B_i \leq B_{i−1}$
   • $B_2 > B_1$，$T_2 = T_1$，$B_{K−1} = B_K$，$T_{K−1} < T_K$
2. “O” 由一个大矩形 $A$，挖去一个小矩形 $B$ 得到，这两个矩形的边都平行于坐标轴。设大矩形 $A$ 左下角的方格坐标为 $(u, v)$，长为 $W$，宽为 $H$，则小矩形 $B$ 满足左下角方格坐标为 $(u + 1, v + 1)$，长 $W − 2$，宽 $H − 2$。要求满足：
   • $W \geq 3, H \geq 3$
   • $u > R_K + 1$
3. “I” 为 $3$ 个边平行于坐标轴的从下到上的实心矩形组成，从下到上依次标号为 $1,2,3$，第 $i$ 个矩形的左下角格子坐标设为 $(P_i, Q_i)$，右上角格子坐标设为 $(G_i, H_i)$，要求满足：
   • $P_i \leq G_i, Q i \leq H_i$
   • $P_1 = P_3 > u + W$，$G_1 = G_3$
   • $Q_1 = H_1 = Q_2 − 1$，$H_2 + 1 = Q_3 = H_3$
   • $P_1 < P_2 \leq G_2 < G_1$

下图是一个 “N”，“O”，“I” 的例子。

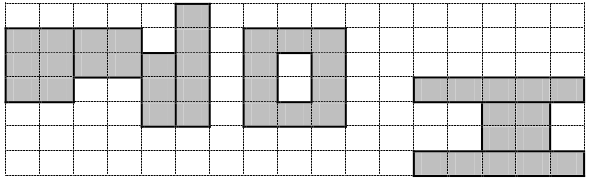
另外，所有画的图形均不允许超过纸张的边界。现在小 E 想要知道，他能画出的最大幸运度是多少。

输入格式

第一行包含两个正整数 $n$ 和 $m$，分别表示矩阵的行数和列数。

接下来 $n$ 行，每行有 $m$ 个整数，第 $i + 1$ 行的第 $j$ 个数表示格子 $(j, n − i + 1)$ 的幸运值。

输出格式

输出一个整数 $T$，表示小 E 能够获得的最大幸运度。

样例一

input

3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1

output

24

样例二

input

3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

output

-20

样例三

见样例数据下载。

限制与约定

对于所有的测试数据，保证 $n \geq 3, m \geq 12$。

时间限制：$2\texttt{s}$

空间限制：$512\texttt{MB}$

下载

样例数据下载