在达芬奇时代，有一个流行的儿童游戏称为连珠线。当然，这个游戏是关于珠子和线的。线是红色或蓝色的，珠子被编号为 $1$ 到 $n$。这个游戏从一个珠子开始，每次会用如下方式添加一个新的珠子：
- Append(w, v)：一个新的珠子 $w$ 和一个已经添加的珠子 $v$ 用红线连接起来。
- Insert(w, u, v)：一个新的珠子 $w$ 插入到用红线连起来的两个珠子 $u, v$ 之间。具体过程是删去 $u, v$ 之间红线，分别用蓝线连接 $u, w$ 和 $w, v$。
每条线都有一个长度。游戏结束后，你的最终得分为蓝线长度之和。
给你连珠线游戏结束后的游戏局面，只告诉了你珠子和链的连接方式以及每条线的长度，没有告诉你每条线分别是什么颜色。
你需要写一个程序来找出最大可能得分。即，在所有以给出的最终局面结束的连珠线游戏中找出那个得分最大的，然后输出最大可能得分。
输入格式
第一行一个正整数 $n$，表示珠子的数量。珠子从 $1$ 到 $n$ 编号。
接下来 $n - 1$ 行每行三个整数 $a_i, b_i, c_i$。保证 $1 \leq a_i < b_i \leq n$。$1 \leq c_i \leq 10000$。表示 $a_i$ 号珠子和 $b_i$ 号珠子间连了长度为 $c_i$ 的线。
输出格式
输出一个整数，表示最大可能得分。
样例一
input
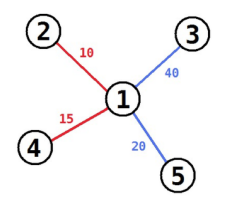
5 1 2 10 1 3 40 1 4 15 1 5 20
output
60
explanation
可以通过如下方式获得 $60$ 分：首先从 $3$ 号珠子开始。
- 把 $5$ 和 $3$ 连起来。（线长度任意）
- 在 $3$ 和 $5$ 之间插入 $1$。（线长分别为 $40$ 和 $20$）。
- 把 $2$ 和 $1$ 用长度为 $10$ 的线连起来。
- 把 $4$ 和 $1$ 用长度为 $15$ 的线连起来。
样例二
input
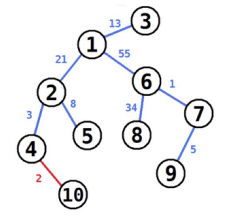
10 4 10 2 1 2 21 1 3 13 6 7 1 7 9 5 2 4 3 2 5 8 1 6 55 6 8 34
output
140
explanation
限制与约定
第一个子任务共 13 分，满足 $1 \leq n \leq 10$。
第二个子任务共 15 分，满足 $1 \leq n \leq 200$。
第三个子任务共 29 分，满足 $1 \leq n \leq 10000$。
第四个子任务共 43 分，满足 $1 \leq n \leq 200000$。
时间限制：$1\texttt{s}$
空间限制：$256\texttt{MB}$
鄂公网安备 42010202000505 号