出题人 02 喜欢研究己酸 $(CH_3(CH_2)_4COOH)$ 的化学性质。
现在平面上有 $n$ 个己酸分子，第 $i$ 个分子位于 $(x_i,y_i)$。己酸分子非常小，因此出题人 02 将其设为了一个点。
出题人 02 总是在想把这些己酸集合在一起会发生什么。所以他会问你 $Q$ 个问题：第 $i$ 个问题中，他想统计出到 $(0,z_i)$ 这一点的欧几里得距离不超过 $R_i$（小于等于 $R_i$）的己酸分子个数。
你作为未来的大理论计算机科学家，当然知道用什么算法和数据结构来解决啦！
输入格式
第一行两个整数 $n,Q$.
接下来 $n$ 行，每行两个整数 $x_i,y_i$。
接下来 $Q$ 行，每行两个整数 $z_i,R_i$。
输出格式
$Q$ 行，第 $i$ 行一个整数表示第 $i$ 次询问的答案。
样例一
input
5 5 -27 -18 -11 10 -29 4 26 26 16 -9 -11 22 -24 15 -19 3 -11 6 -17 24
output
1 0 0 0 1
explanation
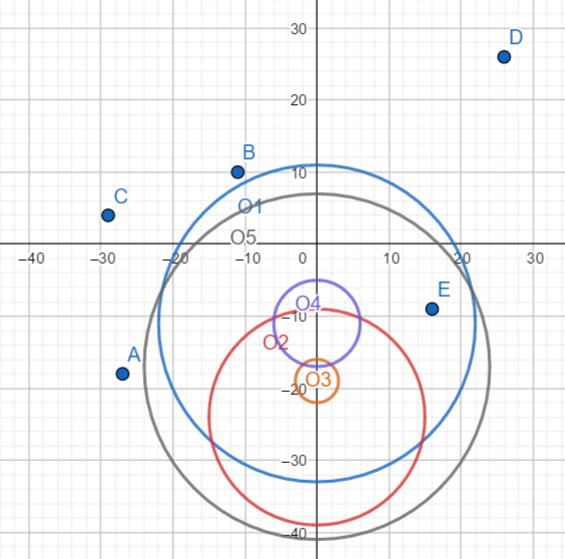
这个样例是随机生成的，所以看上去非常不靠谱。
样例二
见样例数据下载。
该样例数据范围同测试包 1。
样例三
见样例数据下载。
该样例数据满足 $x_i,y_i,z_i$ 均在 $[-10^5,10^5]$ 均匀随机生成，$R_i$ 在 $[1,10^5]$ 均匀随机生成。
数据范围
| 测试包编号 | $n$ | $Q$ | 分值 |
|---|---|---|---|
| $1$ | $\le 2000$ | $\le 5000$ | $15$ |
| $2$ | $\le 12000$ | $\le 5 \times 10^5$ | $30$ |
| $3$ | $\le 4000$ | $\le 10^6$ | $20$ |
| $4$ | $\le 7000$ | $20$ | |
| $5$ | $\le 12000$ | $15$ |
对于所有测试数据，满足$1 \le n \le 12000,0 \le Q \le 10^6,|x_i|,|y_i|,|z_i| \le 10^9,1 \le R_i \le 10^9$。
特殊地，测试包 2 中 $x_i,y_i,z_i,R_i$ 均是在上述合法范围内均匀随机生成的。
极限数据输入约 $\texttt{21MB}$，输出约 $\texttt{5MB}$，请选手注意自己 IO 的用时。
时间限制：$4\texttt{s}$
空间限制：$512\texttt{MB}$
鄂公网安备 42010202000505 号