躲过了AlphaGo之后,你躲在SingleDog的长毛里,和它们一起来到了AlphaGo的家。此时你们才突然发现,AlphaGo的家居然是一个隐藏在地下的计算中心!难道AlphaGo如此人赢的秘密是...它其实是一个AI?
根据情报,这个地下的计算中心的结构构成了一棵无根树,整个计算中心名为被AT-field的力场保护起来,保护力场的直径恰好等于树的直径(树的直径定义为树上距离最远的两个结点之间的距离,结点
由于保护力场的存在,SingleDog们每次只能进入整棵树的一个叶子(度为1的结点),由于狗的大脑很小,他们每次只会随机进攻一个原树的叶子,并且破坏里面的设备,更加狼狈的是他们甚至会重复进入一个已经被破坏过的叶子。
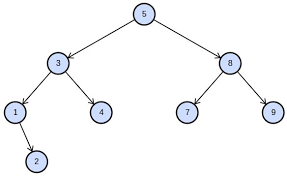
比如这棵树中,SingleDog们攻击的就是
他们想知道,期望多少次之后,可以使得保护力场的直径缩小?
即,对于一棵树,每次随机染黑一个叶子(可能会重复染黑),期望多少次后直径变小?
输入格式
从标准输入读入数据。
第一行一个正整数
接下来
输出格式
输出到标准输出。
输出一行一个整数表示答案在模
即设答案化为最简分式后的形式为
样例一
input
3 1 2 2 3
output
1
样例二
input
6 1 2 2 3 1 4 4 5 1 6
output
499122178
样例三
见样例数据下载。
样例四
见样例数据下载。
限制与约定
对于所有数据,
为了拿到每个子任务的分数,你必须通过所有他依赖的子任务。
| 子任务 | 分值 | 特殊性质 | 依赖的subtask | |
|---|---|---|---|---|
| 1 | 12 | 无 | 无 | |
| 2 | 18 | 无 | ||
| 3 | 20 | 树上任意两点距离(距离定义为两点间最短路边的条数) |
无 | |
| 4 | 15 | 任意点度数 |
无 | |
| 5 | 35 | 无 |
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号