Scape非常喜欢在和Mythological逛公园的时候,讲时间复杂度的知识给她听。但是他很快便伤心地发现Mythological对复杂度的兴趣,还没有旁边的蚯蚓列队表演的兴趣高,只好向whx诉苦。
whx面对Scape的疑惑,告诉他,重要的是Mythological喜欢什么,而不是他自己喜欢什么。Scape发现Mythological特别喜欢玩Geometry Dash,所以特意下载了一个来玩。
打开游戏,Scape发现平面直角坐标系上有
Scape很快反应过来,以原点
如果一个三角形的内部不包含任何蓝点,Scape称该三角形是空的,否则,Scape称该三角形是非空的。
Scape的任务是判断以原点和任意两个红点为顶点构成的
任务
你需要编写一个函数 check_triangles,以完成题目的任务:
- check_triangles(n, m, rx, ry, bx, by, result)
- n: 坐标系上给出的红点个数。
- m: 坐标系上给出的蓝点个数。
- rx: 大小为
- ry: 大小为
- bx: 大小为
- by: 大小为
- result: 大小为
实现细节
本题只支持 C/C++。
你只能提交一个源文件实现如上所述的 check_triangles 函数,并且遵循下面的命名和接口。你需要包含头文件 triangles.h。
void check_triangles(int n, int m, int *rx, int *ry, int *bx, int *by, int **result);如果有不清楚的地方,见样例及测评库下载,内附了样例程序。
评测方式
评测系统将读入如下格式的输入数据:
- 第
- 第
- 第
- 第
对于样例数据,
对于测试数据,
注意:
样例一
input
1 4 3 3 3 -2 4 5 -5 -4 -2 3 -1 1 0 -3 -2
output
-1 0 -1 1 -1 2
explanation
如下图所示:
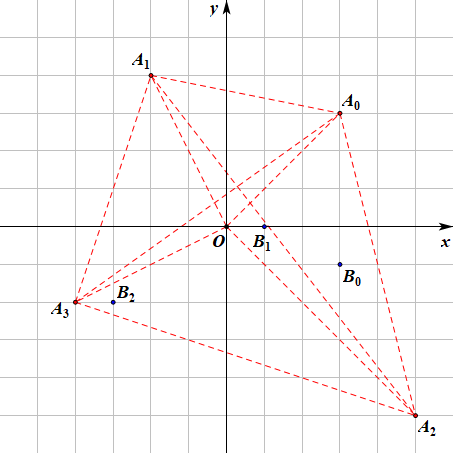
样例输出中 result[0][2]=0 可以改成 1,这是因为
样例二
见样例及测评库下载。该样例输出共包含
样例三
见样例及测评库下载。该样例输出共包含
限制与约定
对于所有数据,
为避免精度误差,保证任意三点构成的夹角在
| 子任务 | 分值 | ||
|---|---|---|---|
| 1 | 32 | ||
| 2 | 46 | ||
| 3 | 22 |
时间限制:
空间限制:

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号