土卫二上一片荒凉，但这不影响基地的建造速度。在伏特跳蚤国王的指挥下，跳蚤们愉快地和从火星抓来的特有生物 “火猩” 一起高速建造基地。

短短几天，基地便建造完毕，这标志着跳蚤国土卫二外区设立完毕。

这么大的事怎么能不庆祝呢？于是跳蚤们做了一桌丰盛的蚤餐。蚤餐的话当然少不了跳蚤的最爱 —— 仙人掌蛋糕啦！由于火猩巨大的生产力，这个蛋糕是无限大的。在切下 $n$ 刀之后，蛋糕被分为了很多块。面积有限的蛋糕块准备分给跳蚤吃，面积无限大的蛋糕块则准备分给火猩吃。这时……

从某个隐蔽的角落射出了一束耀眼的光芒，这束光巧妙避开了所有蛋糕块的顶点，所经过的 $n + 1$ 个蛋糕块都被破坏了。

“高稳鸡光！”众蚤惊呼了起来。

没错，这意味有几个黑恶势力的特工混进了火箭中，也随着跳蚤大军来到了土卫二，虽然很快就被伏特跳蚤国王抓住并拿去煲汤了……

回过头来，伏特跳蚤国王想统计下每个被高稳鸡光破坏了的蛋糕块是准备给跳蚤吃的，还是准备给火猩吃的。

一句话题意：平面上有 $n+1$ 条直线，前 $n$ 条直线把平面分成许多块，这些块有些面积有限，有些面积无限，而第 $n+1$ 条直线不经过前 $n$ 条直线的交点，且一定不和前 $n$ 条直线中的任意一条平行，求第 $n+1$ 条直线被前 $n$ 条直线划分成的 $n+1$ 段中哪些在面积有限的块里，哪些在面积无限的块里。

输入格式

第一行一个正整数 $n$，意义如前所述。

接下来 $n+1$ 行，第 $i$ 行 $4$ 个整数 $x_1, y_1, x_2, y_2$ 表示第 $i$ 条直线经过 $(x_1,y_1)$ 和 $(x_2,y_2)$ 两点。

保证第 $n+1$ 条直线不经过前 $n$ 条直线的交点，且一定不和前 $n$ 条直线中的任意一条平行或重合。

保证第 $n+1$ 条直线不与 $x$ 轴垂直，且对于第 $n + 1$ 条直线有 $x_1 < x_2$。

输出格式

输出一行长度为 $n+1$ 的 01 串，第 $x$ 个数字如果为 $0$ 则表示第 $x$ 段是在面积无限的块里，如果为 $1$ 则表示第 $x$ 段是在面积有限的块里。

请注意，段的输出顺序必须是从左到右。由于第 $n + 1$ 条直线不与 $x$ 轴垂直，所以从左到右的顺序总是存在的。

样例一

input

3
0 0 1 0
0 1 1 2
0 1 1 0
-5 0 5 1

output

0010

explanation

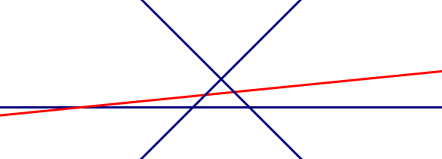
样例二

input

3
0 0 1 0
0 1 1 1
0 2 1 2
0 0 1 1

output

0000

explanation

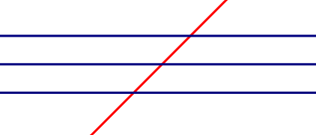
注意数据中前 $n$ 条直线可能出现互相平行的情况。

样例三

input

4
0 0 1 0
0 1 1 1
0 0 1 1
0 1 1 2
-5 0 5 1

output

00100

explanation

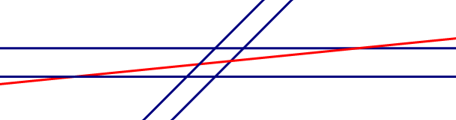
样例四

见样例数据下载。

限制与约定

由于一些原因，本题使用捆绑测试。每个子任务有若干个测试点，分为 $6$ 个子任务，你只有通过一个子任务的所有测试点才能得到这个子任务的分数。

在所有数据中，满足 $3 \leq n \leq 10^5$，保证 $-2\times 10^6 \leq x_1, y_1, x_2, y_2 \leq 2 \times 10^6$。

为了避免精度问题，保证第 $n+1$ 条直线和前 $n$ 条直线的 $n$ 个交点中，两两之间的距离不小于 $0.1$。

时间限制：$2\texttt{s}$

空间限制：$256\texttt{MB}$

下载

样例数据下载