楔子
题意:求两个大整数相乘的积.
选手1:我会$\mathsf{unsigned\ long\ long}$!
预计得分:$0\mathsf{pts}$
选手2:我会高精!
预计得分:$30\mathsf{pts}$
选手3:我会$\mathsf{Python}$!
预计得分:$\cdots$
(选手3被众人围殴致死)
卷积思想
引入 1
求两个无符号整数相乘的积.
在这里,我们并不是想编写一个程序来实现上述功能,而是老老实实用纸笔计算.
例:
计算 $21\times121$
解: $$\quad\ \ 21$$ $$\times\ 121$$
$$\quad\ \ 21$$ $$\ 42$$ $$\!\!\!\!21$$
$$\!2541$$
答:$21\times121=2541.$
回顾刚才的计算过程,我们分析一下$2541$的每一位数字是怎么得出来的.
$1=1\times1$
$4=2\times1+2\times2$
$5=2\times2+1\times1$
$2=2\times1$
我们用数组$A$存储$21$这个数,$B$存储$121$,$C$存储答案,则
$C_0=A_0\times B_0$
$C_1=A_1\times B_0+A_0\times B_1$
$C_2=A_1\times B_1+A_0\times B_2$
$C_3=A_1\times B_2$
观察下标,我们发现两个正整数相乘的结果满足下面规律:
$$ C_k=\sum^k_{i=0}A_i\times B_{k-i} $$
引入 2
求两个多项式相乘的积.
同上例,我们依然用纸笔计算之.
例:
计算$(1+2x)(1+2x+x^2)$
解:
$(1+2x)(1+2x+x^2)=1+2x+x^2+2x+4x^2+2x^3=1+4x+5x^2+2x^3$
根据计算过程分析各项系数,有:
$1=1\times1$
$4=2\times1+2\times2$
$5=2\times2+1\times1$
$2=2\times1$
这里我们用数组$A$存储$(1+2x)$的系数,$B$存储$(1+2x+x^2)$的系数,$C$存储答案的系数,则:
$C_0=A_0\times B_0$
$C_1=A_1\times B_0+A_0\times B_1$
$C_2=A_1\times B_1+A_0\times B_2$
$C_3=A_1\times B_2$
我们发现,两个多项式乘积的系数满足下面的规律:
$$ C_k=\sum^k_{i=0}A_i\times B_{k-i} $$
卷积?!
我们观察上面两个式子,可以看出它们具有相同的形式,我们称这种形式为卷积.
形象理解:
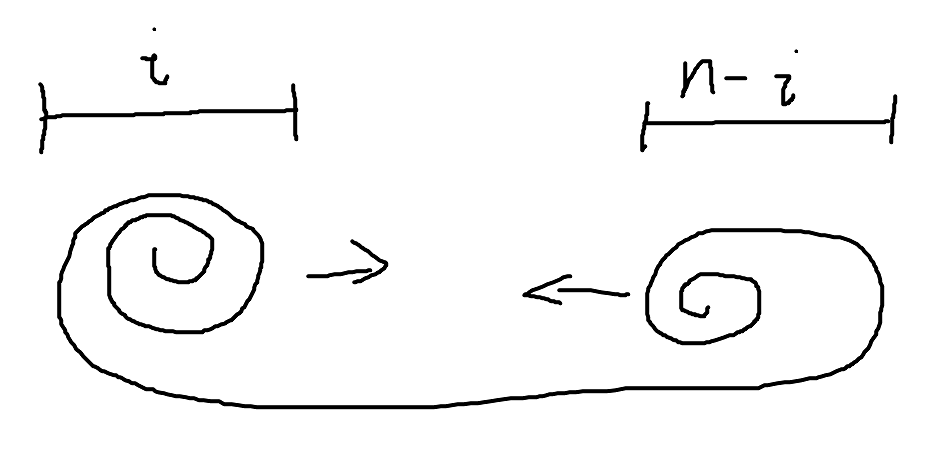
“卷积”,“积”自然指乘积,而“卷”的含义如图:
第一次尝试
#include<cmath>
#include<cstdio>
const int N = 1000005, mod = 998244353;
int A[N], B[N], C[N];
int a, b;
void mutiply()
{
for(int k = 0; k < a + b - 1; ++k)
for(int i = 0; i <= k; ++i)
C[k] += (A[i]*B[k-i]);
}
int main()
{
scanf("%d%d",&a,&b);
++a,++b;
for(int i=0;i<a;++i)scanf("%d",A+i);
for(int i=0;i<b;++i)scanf("%d",B+i);
mutiply();
for(int i=0;i<a+b-1;++i)printf("%d ",C[i]);
return 0;
}干得漂亮!我们收获了$44\mathsf{pts}$的佳绩!
另一种方法
之前有用到这样一个思路,对于任意多项式$F$,我们可以采用将其升幂排列,再存储其系数的办法来表示出$F$.
这里谈谈另外一种办法.
众所周知,两点确定一条直线,用解析几何的语言描述,就是 $y=ax+b$由两个有序点对${(x_0,y_0),(x_1,y_1)}$唯一地确定.
为什么?因为我们知道了这两个点的坐标,将其带入进解析式,得到二元一次方程组,再解这个方程组,得到$a$和$b$的值.
当$y=ax^2+bx+c$时呢?进一步地,当$y=a_0x^0+a_1x^1+\cdots+a_nx^n$时呢?
我们可以看出,式子$y=a_0x^0+a_1x^1+\cdots+a_nx^n$有$(n+1)$个系数,如果我们要唯一地确定它,就需要$(n+1)$个点的坐标联立起来解出系数.
也就是说,$(n+1)$个有序点对可以唯一表示一个多项式,我们称其为“点值表示法”
但是
它有什么用?我们知道,将两个浮点数相乘的时间复杂度是$O(1)$的,那么,假设我们有两个多项式$A$和$B$,不妨设它们为$(1+2x)$和$(1+2x+x^2)$,接下来,我们计算它们在一些点上的值: $$ x\quad A\quad B $$ $$ 0\quad\ 1\quad\ 1 $$ $$ 1\quad\ 3\quad\ 4 $$ $$ 2\quad\ 5\quad\ 9 $$ $$ 3\quad7\quad16 $$ $$ 4\quad9\quad25 $$ 将$A$列和$B$列对应的数相乘,记作$C$列,则 $$ x\quad C $$ $$ 0\quad\ 1 $$ $$ 1\quad12 $$ $$ 2\quad45 $$ $$ 3\ \ 112 $$ $$ 4\ \ 225 $$ 在上面我们求得$A\times B$,我们将$x={0,1,2,3,4}$代入$A\times B$, $$ x\quad A\times B $$ $$ 0\quad\quad\quad\ 1 $$ $$ 1\quad\quad\quad12 $$ $$ 2\quad\quad\quad45 $$ $$ 3\quad\quad\ \ 112 $$ $$ 4\quad\quad\ \ 225 $$
相等?!
是的,当我们转换为点值表示法时,两个多项式在某点上的值的乘积等于两个多项式的乘积在某点上的值.(显然$F(x)\times G(x)=F(x)\times G(x)$,等号左边是点值表示法的$F$和$G$在$x$处的值的乘积,等号右边是它们的乘积在$x$处的值,慢慢品味.)
设这两个多项式是$m$和$n$次的,则它们的乘积是$(m+n)$次的,所以,我们只要计算这两个多项式在$(m+n+1)$个点上的值并一一相乘,就可以确定这两个多项式的乘积.
时间复杂度?$O(n+m)\qquad\mathsf{Good\ Job!}$
且慢
$1)$如何将点值表示法转换为系数表示法?
$2)$我们该如何选取那些待计算的点?显然,我们需要在这些点上计算它的平方,立方甚至更高次方,而且,如果我们能合理地选择待计算的点,那么计算将会极大地简化.
接下来我们将会看到一类名叫单位根的复数,结合分治思想后可以将时间复杂度降低到$O(n\log n)$.
但首先,我们还是要了解$\cdots$
复数
复数是形如$a+bi$的数,其中$a,b\in\mathrm{R},i=\sqrt{-1}$.
将全体复数的集合称作$\mathrm{C}$
复数的三则运算(除法现在还用不到)
- $(a+bi)+(c+di)=(a+b)+(c+d)i$
- $(a+bi)-(c+di)=(a-b)+(c-d)i$
- $(a+bi)\times(c+di)=(ac-bd)+(bc+ad)i$
证明:注意$i^2=-1$,利用结合律,分配律即证.
注:复数也满足结合律,分配律和幂运算规则.
欧拉公式和单位根
欧拉公式:$e^{i\theta}=\cos\theta+i\sin\theta$
注意到$e^{(2a+1)\pi i}=-1,e^{2a\pi i}=1,a\in\mathrm{N}$
则方程$x^n=1$的根(称作单位根,记作$\omega^k_n$)为 $$ \omega^k_n=e^{\frac{2k\pi}{n}i}=\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n} $$ 证明:由$(a^x)^p=a^{xp}$结合欧拉公式即证得其为方程的根.
单位根的性质
$1)\omega^k_n=\omega^{k\%n}_n$
证:$\omega^k_n=\cos\dfrac{2k\pi}{n}+i\sin\dfrac{2k\pi}{n}=\cos\dfrac{2(k\%n)\pi}{n}+i\sin\dfrac{2(k\%n)\pi}{n}=\omega^{k\%n}_n$
其中倒数第二步是当$k\ge n$时,将$k$约去得到$k\%n$.
$2)\omega^k_n=(\omega^1_n)^k$
证:$\omega^k_n=e^{\frac{2k\pi}{n}i}=e^{\frac{2\pi}{n}i\times k}=(e^{\frac{2\pi}{n}i})^k=(\omega^1_n)^k$
$3)\omega^0_n=1$
证:$\omega^0_n=\cos0+i\sin0=1+0i=1$
$4)\omega^k_n\times \omega^j_n=\omega^{k+j}_n$
证:$\omega^k_n\times \omega^j_n=(\omega^1_n)^k\times(\omega^1_n)^j=(\omega^1_n)^{k+j}=\omega^{k+j}_n$
$5)\omega^{pk}_{pn}=\omega^k_n$
证:$\omega^{pk}_{pn}=e^{\frac{2pk\pi}{pn}i}=e^{\frac{2k\pi}{n}i}=\omega^k_n$
$6)\omega^{k+\frac{n}{2}}_n=-\omega^k_n$
证:$\omega^{k+\frac{n}{2}}_n=\omega^{\frac{2k+n}{2}}_n=e^{\frac{(2k+n)\pi}{n}i}=e^{\frac{2k\pi}{n}i+\pi i}=e^{\frac{2k\pi}{n}i}\times e^{\pi i}=-e^{\frac{2k\pi}{n}i}=-\omega^k_n$
回到多项式
关于复数和单位根的性质已经说得够多了,现在把注意力放到多项式中.
前面有提到分治思想,现在我们来好好研究一下.
设多项式$F(x)=a_0x^0+a_1x^1+\cdots+a_{n-1}x^{n-1}=\sum^{n-1}_{i=0}a_ix^i$,则它可以唯一地表示成两个多项式的和.哪两个?请看: $$ F(x)=\sum^{n-1}_{i=0}a_ix^i=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}x^{2i}+\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}x^{2i+1} $$ 即:按照次数的奇偶性将多项式$F$分成$L,R$两个部分.
那么,为什么要这么分?请继续向下看.
记 $$ L(x)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}x^{i} $$ $$ R(x)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}x^{i} $$ 则 $$ F(x)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}x^{2i}+\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}x^{2i+1}=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}(x^2)^i+\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}(x^2)^i\times x=L(x^2)+xR(x^2) $$
重头戏
这里$F$是$(n-1)$次的多项式,需要$n$个点来确定.
将单位根$\omega^k_n$代入 $$ F(x)=L(x^2)+xR(x^2) $$ 得 $$ F(\omega^k_n)=L(\omega^{2k}_n)+\omega^k_nR(\omega^{2k}_n) $$ 即 $$ (1):\qquad F(\omega^k_n)=L(\omega^{k}_{\frac{n}{2}})+\omega^k_nR(\omega^{k}_{\frac{n}{2}}) $$ 则我们得到了$F(x)$在$\omega^0_n,\omega^1_n,\cdots,\omega^{\frac n2-1}_n$这$\dfrac n2$个点上的值.
那另外$\dfrac n2$点上的值呢?
将单位根$\omega^{k+\frac n2}_n$代入 $$ F(x)=L(x^2)+xR(x^2) $$ 得 $$ F(\omega^k_n)=L(\omega^{2k+n}_n)+\omega^{k+\frac n2}_nR(\omega^{2k+n}_n) $$ 即 $$ F(\omega^k_n)=L(\omega^{2k}_n)+\omega^{k+\frac n2}_nR(\omega^{2k}_n) $$ 即 $$ (2):\qquad F(\omega^k_n)=L(\omega^{k}_{\frac{n}{2}})-\omega^k_nR(\omega^{k}_{\frac{n}{2}}) $$ 则我们得到了$F(x)$在$\omega^{\frac n2}_n,\omega^{\frac n2+1}_n,\cdots,\omega^{n-1}_n$这另外$\dfrac n2$个点上的值.
对比$(1)$和$(2)$,可以看出它们之间只差了一个正负号.
所以只要知道$L$和$R$在$\omega^0_{\frac n2},\omega^1_{\frac n2},\cdots,\omega^{\frac n2-1}_{\frac n2}$的值,就可以在$O(n)$的时间复杂度内唯一地确定$F$.
那么,如何求得$L$和$R$在这些点上的值呢?
注意到:$L$和$R$都是$\dfrac n2$项的多项式!
分治
所以,我们将规模为$n$的多项式求值问题分解成了规模为$\dfrac n2$的子问题!
递归地求解即可.
一个小细节:为了避免出现$2\nmid n$的情况,我们强行向高位补零,补成一个具有$2^k$项的多项式.
综合运用
这就是$\mathsf{DFT}$:离散傅里叶变换!
代码实现:
void dft(comp *f,int len)
{
if(len==1)return ;
comp *fL=f,*fR=f+len/2;
for(int k=0;k<len;k++)G[k]=f[k];
for(int k=0;k<len/2;k++)L[k]=G[k<<1],R[k]=G[k<<1|1];
dft(L,len/2);
dft(R,len/2);
comp W(cos(2*pi/len),sin(2*pi/len)),b(1,0);
for(int k=0;k<len/2;k++)
{
G[k]=L[k]+b*R[k];
G[k+len/2]=L[k]-b*R[k];
b*=W;
}
for(int k=0;k<len;k++)f[k]=G[k];
}反过来
设$G(z)=\mathcal{F}[F(x)]$,则$F(x)=\mathcal F^{-1}[G(z)]$.
其中$\mathcal F$称作(离散)傅里叶变换,$\mathcal F^{-1}$称作(离散)逆傅里叶变换,又称$\mathsf{IDFT}$.
$\mathsf{I}:\mathsf{Inversed}$
结论:
($f_i,g_i$为$F,G$第$i$项的系数)
$$ nf_k=\sum^{n-1}_{i=0}\omega^{-ki}_ng_i $$
负数次单位根?
由定义知$\omega^{-k}_n=(\omega^{-1}_n)^k$
那么$\omega^{-1}_n=\cos-\dfrac{2\pi}{n}+i\sin-\dfrac{2\pi}{n}=\cos\dfrac{2\pi}{n}-i\sin\dfrac{2\pi}{n}$
证明?诱导公式!
优化
将递归转换为循环,避免数组的拷贝,我们可以写出以下代码,这就是经典的快速傅里叶变换!
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const int N = 5100000, mod = 998244353;
const double pi=acos(-1);
int n,m;
struct comp
{
comp (double _a=0,double _b=0){a=_a,b=_b;}
double a,b;
comp operator + (comp const &B) const
{return comp(a+B.a,b+B.b);}
comp operator - (comp const &B) const
{return comp(a-B.a,b-B.b);}
comp operator * (comp const &B) const
{return comp(a*B.a-b*B.b,a*B.b+b*B.a);}
}F[N],G[N];
int t[N];
void fft(comp *f,bool flag)
{
for (int i=0;i<n;i++)
if (i<t[i])swap(f[i],f[t[i]]);
for(int p=2;p<=n;p<<=1)
{
int len=p>>1;
comp W(cos(2*pi/p),sin(2*pi/p));
if(!flag)W.b*=-1;
for(int k=0;k<n;k+=p)
{
comp b(1,0);
for(int l=k;l<k+len;l++)
{
comp temp=b*f[len+l];
f[len+l]=f[l]-temp;
f[l]=f[l]+temp;
b=b*W;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=0;i<=n;i++)scanf("%lf",&F[i].a);
for (int i=0;i<=m;i++)scanf("%lf",&F[i].b);
for(m+=n,n=1;n<=m;n<<=1);
for(int i=0;i<n;i++)t[i]=(t[i>>1]>>1)|((i&1)?n>>1:0);
fft(F,1);
for(int i=0;i<n;++i)F[i]=F[i]*F[i];
fft(F,0);
for(int i=0;i<=m;++i)printf("%d ",(int)(F[i].b/n/2+0.49));
return 0;
}三次变两次优化
上面的代码中有体现
设 $P=F+iG$
则 $P^2=F^2-G^2+2iFG$
即,将输入当作一个多项式的实部和虚部,将其$\mathsf{FFT}$后自乘,再$\mathsf{IFFT}$回来,输出就是虚部除以$2$
最终尝试
习题和拓展阅读
$$ \mathrm{END.} $$

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号